The SHL Numerical Reasoning Test is considered SHL’s most challenging and intimidating test. The test comprises 10 questions within 18 minutes and evaluates your ability to calculate, analyse, and interpret numerical data.
To help you pass your SHL Numerical Reasoning Test, we have also developed a dedicated PrepPack to ensure you will be fully prepared and confident on test day. Our PrepPack includes 3 full-length SHL Numerical Interactive Simulations that closely replicate the real exam; 30+ numerical-focused practice tests; tailored and specific SHL Numerical test guides, and much more.
Use our accurate SHL Numerical Test simulation to gain a feel for the real exam.
What Is the SHL Numerical Reasoning Test?
The SHL Numerical Reasoning Test evaluates your ability to calculate, analyse, and interpret numerical data.
Your SHL Numerical Reasoning Test may be in 1 of 3 versions, which differ in question types, difficulty, and time limits. To be properly prepared, it is crucial to know which version you take.
Don't worry; we'll explain everything further below.
The three versions of the SHL Numerical Test are:
- SHL Verify Numerical Reasoning Test (Interactive) - 10 questions in 18 minutes
- SHL Verify Numerical Reasoning Test (Next Generation) - 16 questions in 18-20 minutes
- SHL CEB Verify Numerical Reasoning (Legacy Generation) - 18 questions in 17-25 minutes. This test is less common but is still occasionally used.
Preparing for the right test version is absolutely crucial for succeeding on your SHL Numerical Test. Find Which SHL Test Version You Have in 3 Steps and ensure you are not wasting your preparation time.
Below we will go over each test separately, alongside sample questions with full explanations and a free sample test.
SHL Verify Numerical Reasoning Test (Interactive)
The SHL Verify Interactive Numerical Reasoning Test is one of SHL’s new assessments and is currently the most common version. While it’s much more engaging for the test-takers, it is also more complex and takes longer to solve. That’s because you have to consume long instructions, analyse data, make calculations, and finally tweak and interact with graphs, charts, and pies.
The test allows a calculator and contains 18 questions to be answered in 10 minutes.
The test instructions will specifically say “…an activity-based test that allows you to drag, drop, and interact…”
For more information, see the SHL Test Finding Guide.
SHL Numerical Reasoning Test (Interactive) Sample Question
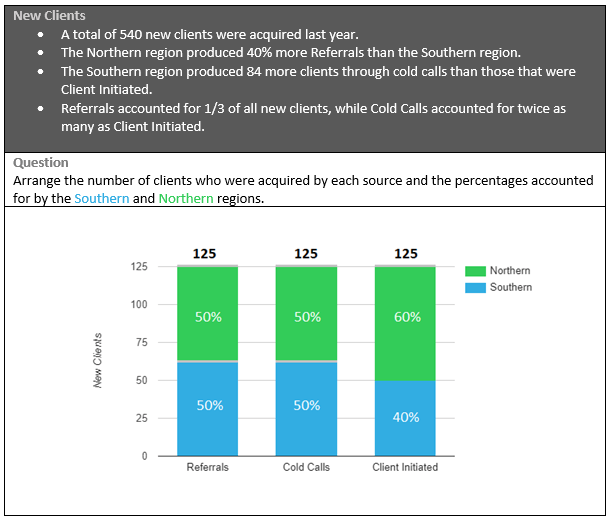
Final Answer:

Pretty similarly to question #3 in this guide – this one is a classic case of systems of equations used to find several variables.
In this case, we have 6 variables – let’s arrange them in a table for convenience:
| Variable | Region | Method |
| NR | Northern | Referrals |
| NC | Northern | Cold Calls |
| NI | Northern | Client-Initiated |
| SR | Southern | Referrals |
| SC | Southern | Cold Calls |
| SI | Southern | Client-Initiated |
Note: This table is for the sake of explanation only. During the real test, don’t spend time arranging it, and simply name the variables as is most convenient for you.
Out of the 4 data items, the first and last ones on the list are the best place to start, as they can immediately reveal the number of clients in each method.
Let’s dismantle these pieces of data to their components:
A total of 540 new clients were acquired this year
Referrals accounted for 1/3 of all new clients

Therefore, Cold Calls and Client-Initiated account for the remaining 2 thirds of new clients:
Cold Calls + Client-Initiated = 540 - 180 = 360
Using the last bit of information - Cold Calls accounted for twice as many as Client-Initiated:
2 (Client-Initiated) + Client-Initiated = 360
Client-Initiated = 120 Clients
Cold Calls = 240 Clients
So, we can now rearrange the graph as:

Tip: The pale grey lines above the graph means that you are able to change the value below the line. In this case, the total value of all bars can be changed, but the division of Client Initiated between Northern (60%) and Southern (40%) is pre-determined.
Now, let’s form some other equations using the other data items.
We should try and focus on data items containing the least variables. Data item 2 is the best for this purpose:
The Northern region produced 40% more Referrals than the Southern region.
Or in the form of an equation:
(I) NR = 1.4 x SR
We already know the total number of referrals:
(II) NR + SR = 180
Plugging (I) into (II):
2.4 x SR = 180
SR = 75
NR = 105
Converting to percentages (Don’t forget that!):

And again, we can rearrange the graphs as:

It is time to approach the last piece of information – data item 2:
The Southern region produced 84 more clients through cold calls than those that were Client Initiated.
Or in the shape of an equation:
SC = SI + 84
Since we already know the percentages in the Client-Initiated bar, we can easily deduce SI:
SI = 0.4 x 120 = 48
Plugging into the previous equation:
SC = 48 + 84 = 132
Again, converting into percentages:

And rearranging the graph to its final position:

Feel Like You're Not Ready Yet?
Our SHL Numerical Interactive PrepPack contains comprehensive preparation materials, including:
3 Full-Length SHL Numerical Interactive Simulations - Mimicking the real SHL Numerical Exam, so you'll get to practice the real-time constraints, format, and difficulty level to determine your weak spots. Includes a tailored SHL Numerical Interactive guide.
30+ Additional Numerical-Focused Practice Tests - Allowing you to practice your weak spots and topics revealed in the simulations to improve your numerical skills and general readiness for the test. Our practice tests cover all questions and skills necessary to succeed in the SHL Numerical Test.
10+ SHL Study Guides & Video Tutorials - Giving you a professional grasp of the theory behind each test section and the best ways to solve questions.
SHL Verify Numerical Reasoning Test (Multiple-Choice)
The SHL Verify Multiple-Choice Numerical Reasoning Test is a classic multiple-choice assessment. Here, you usually face tables, graphs, or charts with some data on them, and you need to choose the correct answer — no interactions, tweaking, or games.
The test usually allows a calculator and contains 16 questions to be solved in 20 minutes.
If the test instructions say "After each question, there are four or five response options.” And “Click on the answer…”
For more information, see the SHL Test Finding Guide.
SHL Numerical Reasoning Test (Multiple-Choice) Sample Question
What proportion of both sites' April and May traffic was for Cuisine.net?

Final Answer:
The correct answer is (E) - 38.1%
To calculate this, we add up the total page views of cuisine.net for April and May and divide this amount by the total hits of both sites for the same period.
Therefore, the calculation would be:
(35+45)/(35+45+70+60), which is 80/210 -> 38.1%
Want more? Check out our free SHL Numerical Reasoning (Interactive) sample test or the complete SHL free practice test!
SHL CEB Verify Numerical Reasoning Test
The SHL CEB Numerical Reasoning test is the oldest version of the SHL Numerical Reasoning Test. It is increasingly becoming obsolete, but several employers still use it.
The test contains 18 questions to be solved in 25 minutes.
This version is much easier to identify because you’ll see CEB’s logo in the top left corner of the instructions screen.
CEB SHL Numerical Reasoning Sample Question

How many GBP can be purchased for 7500 CAD?
Final Answer:
7500 CAD*0.6369=4776.75 GBP.
This means you can buy 4776 GBP with 7500 CAD since you don't quite have enough CAD to buy 4777 GBP.
Learn more about the SHL CEB Numerical Reasoning Test.
Should You Use SHL's Direct Numerical Practice?
In the official assessment email, SHL invites you to try sample numerical questions and practice tests using its preparation site, SHL Direct.
Here are three reasons why you can't count on SHL Direct practice tests alone:
#1 They don’t tell you which version to practise (you’ve already learned there are three different versions). Also, you can only complete their practice test once, and to retake it, you'll need to use a different email every time.
#2 You don’t get to see what questions you got wrong or get any solutions or explanations (yes, that’s annoying). But hey, we did that for you! Check out the full solution to SHL's Numerical Reasoning Practice Test.
#3 The practice tests don’t include the wide variety of questions you’ll see on the real test. Additionally, the difficulty level of the practice material is easier. In fact, SHL says on their site that the “difficulty level of the practice tests may not exactly reflect the level of difficulty of the test you will be asked to complete.”
So, you can use the SHL direct numerical practice as a supplement, but for the reasons listed above, we would not recommend relying solely on these tests as these will likely not represent the exact test you'll face. Instead, use more comprehensive practice tests that reflect the difficulty level and format of the actual test.
Ace Your Job Search with a Custom Prep Kit
Job hunting doesn't have to be stressful.
Prepare smarter and ace your interviews faster with our Premium Membership.



How to Get Answers to the Real SHL Numerical Test?
If you're looking for a cheat sheet that has all the answers to the actual SHL Numerical Reasoning test, we have bad news for you.
The bad news is that we don't have a magic PDF with all the answers to the actual assessment.
In fact, no one on the internet has (and don't let them tell you otherwise).
SHL holds a question bank of hundreds of numerical reasoning questions that change with time. And getting your hands on this question bank is impossible.
How to Know Which SHL Numerical Test Version You’ll Be Taking?
The SHL Numerical test is sent to candidates either as a standalone test, like the Amazon SHL Numerical Reasoning test, or as part of the larger SHL General Ability test, like the Rolls Royce Assessment Test (also including Inductive and Deductive sections).
Now, the assessment invitation you get from SHL is one of the vaguest parts of your recruitment process.

Your test invitation will include the assessment’s name, the overall time limit, and what you’re allowed to use (i.e., pen and paper).
That said, this email won’t reveal which of the three versions you’ll be taking and what you’re up against. For example, you won’t be able to distinguish if you got the interactive version or the non-interactive one.
For that, you’ll need to click on the assessment’s link and read the assessment’s intro and instructions.
(don’t worry, clicking on the link won’t start the test)

In the next screen, you’ll see three details that will help uncover the test you’re about to take.
- No. of questions
- Time limit
- Instructions/guidelines
Use the overview of the different tests above to uncover the test version you’re going to take.
Identifying which SHL Numerical test version you’ll be taking is key because it impacts your whole practice process. That said, don’t worry if you can’t detect your version since we have got you covered with a complete preparation pack for all three tests mentioned above.
How the SHL Numerical Tests are Scored & What Are the Result’s Key Takeaways
Once you complete the SHL Numerical assessment, you’ll receive a “Candidate Assessment Report” that includes both feedback and scoring.
Note that the SHL Numerical Reasoning test scores are comparative.
This means that your scores are being compared to a large group of candidates who took these tests in the past (graduates/interns/seniors, etc.).
There are five percentile scores, from A to E, and your score will be placed in one of them, as you can see in this illustration:

The higher you score, the closer you’ll be to group “A”, meaning chances are high that you’ve passed the test.
Generally, it’s safe to say that the pass mark is around 80%; in this case, it’s group “B” and above.
5 Tips and Tricks to Boost Your SHL Numerical Reasoning Test Score
- The SHL Numerical tests include lots of chart question types. When dealing with two-axes charts, be aware of: Time elements (days, months, years etc. that will mostly appear on the horizontal ("X") axis, and Quantity elements that will mostly appear on the vertical ("Y") axis.
Axes being swapped around or mismatched are one of the most common things you’ll encounter on the test, so pay extra attention to this. - Ensure you read the questions carefully and don’t rush to choose a potentially wrong answer, as this is where many candidates tend to fall. To lower the chances of getting a question wrong when time’s running out, use the educated guessing technique (explained in detail in our preparation pack).
- If you have enough prep time before the test, ensure you have strong maths foundations, especially if you’ve been out of school for a while. Tripping on small things like decimals, fractions, and percentages conversions would be a real shame.
- Ensure not to leave any blank questions. Every question left unanswered will result in score reduction.
- Avoid generic Numerical Reasoning practice tests like the plague. The internet is packed with Numerical practice materials that look nothing like the real SHL tests. They might be good for practising your overall numerical reasoning skills, but they are no good for learning what to expect on the actual test.
Other SHL Tests
The most common SHL tests are the Cognitive SHL Verify Interactive, the Verify General Ability (G+), the SHL Numerical Reasoning Test, and the SHL Inductive Reasoning test.
Other less common psychometric tests from SHL include the SHL Verbal, SHL Deductive, SHL Checking, SHL Calculation, SHL Personality Questionnaire (OPQ), SHL SJT (Situational Judgement Test), and SHL Mechanical Comprehension Test.
How Hard Is the SHL Numerical Reasoning Test?
The most challenging elements of the SHL Numerical Reasoning test are the time frame and the information overload that some questions present. You’ll often have little more than 60 seconds to answer every question. A slight misreading of a question will cause you to lose marks.
How to Practise for the SHL Numerical Test
Based on thorough research, our psychometric experts' team has created accurate practice tests designed to get you ready for the SHL Numerical assessments. This is the only practice that simulates the increasingly popular interactive version of the test.
How will this improve your score?
- Cover different question types to be ready for any question on the test, with practice questions and explanations customized to your test version. This exclusively includes the new Verify G+ Interactive version.
- Get more confident and quick when solving questions under time pressure by practicing questions at the same difficulty level and time limit as in the actual test.
- Refresh your math skills with simple and easily digestible math video tutorials and study guides, in case you run into math subjects you haven’t touched in years and want to review the basics from square one.
More Free Practice
We at JobTestPrep find the assessment tests world highly diverse and fascinating. If you are looking to deepen your knowledge in the aptitude tests world, or you want some extra practice before your test, we've got you covered!
Check out these fantastic free practice tests (all are completely free):
Free Aptitude Test | Free Psychometric Test | Free Numerical Reasoning Test | Free Verbal Reasoning Test | Free Cognitive Test | Free Critical Thinking Test | Free Abstract Reasoning Test | Free Spatial Reasoning Tets | Free Personality Test | Free Inductive Test | Free Mechanical Reasoning Test




