The following guide presents answers and full solutions for SHL’s Numerical Reasoning Practice Test (Mobile-Enabled Interactive Ver) from SHL’s official website, followed by essential keynotes regarding the SHL test platform, SHL Talent Central.
The SHL Numerical Reasoning Interactive Test is commonly used by employers across various industries to assess a candidate's numerical abilities. The test is particularly relevant for positions that require strong quantitative skills, like finance, accounting, data analysis, engineering, etc. It comprises 10 questions within a time limit of 18 minutes.
Scroll down to answer SHL Numerical Reasoning questions on the page, or simulate the feel of the real exam by taking a timed, pop-up version.
The SHL Numerical Reasoning Practice Test
1. SHL Numerical Reasoning Test Question - Calculations #1
Calculate whether each person has expensed the right amount for their travel. (navigate using the tabs).
Travel expenses per month are calculated as follows:
- First 250 miles: 11 pence per mile.
- Second 250 miles: 10 pence per mile.
- Mile 501 and above: 5 pence per mile.
Final Answer:
- Person A - Correct
- Person B - Incorrect
- Person C - Incorrect
- Person D - Correct
Since we have 4 persons for whom we should calculate, the best and shortest way to do this will be to create a general formula and to plug in the correct numbers for each person.
According to the data given in the top section, the formula should be:
(Miles0-250) x 0.11 + (Miles250-500) x 0.10 + (Miles500+) x 0.05
Intuitive Explanation for the Formula:
If the person has traveled more than 250 miles, then they have covered the entire first milestone (first 250 miles).
If they traveled more than 500 miles, it means they have also covered the second milestone (second 250 miles).
Everything that is left after the first 500 miles will be calculated in the third and last milestone (501 miles and above).
Let’s solve for each person to make it clearer.
Person A
For person A, the data given is:
- (Miles0-250) = 250 miles (Person A traveled more than 250 miles).
- (Miles250-500) = 250 miles (Person A traveled more than 500 miles).
- (Miles500+) = 505 – 500 = 5 miles
Plugging the numbers into the formula above, we gain:
250 x 0.11 + 250 x 0.10 + 5 x 0.05 = £52.75
That means that person A has calculated his or her expenses correctly.
Person B
For person B, the data given is:
- (Miles0-250) = 250 miles (Person B traveled more than 250 miles).
- (Miles250-500) = 330 – 250 = 80 miles (Person B traveled less than 500 miles).
- Since person B traveled less than 500 miles, (Miles500+) is 0 and will be ignored.
Plugging the numbers into the formula above, we gain:
250 x 0.11 + 80 x 0.10 + 5 x 0.05 = £35.50
That means that person B has calculated his or her expenses incorrectly.
Person C
Using the method above:
- (Miles0-250) = 250 miles
- (Miles250-500) = 250 miles
- (Miles500+) = 732 – 500 = 232 miles
Plugging the numbers into the formula above, we gain:
250 x 0.11 + 250 x 0.10 + 232 x 0.05 = £64.10
That means that person C has calculated his or her expenses incorrectly.
Person D
Using the method above:
- (Miles0-250) = 250 miles
- (Miles250-500) = 289 – 250 = 39 miles
Plugging the numbers into the formula above, we gain:
250 x 0.11 + 39 x 0.10 = £31.40
That means that person B has calculated his or her expenses correctly.
Tip: In such questions, it is recommended to take note of commonly used numbers, such as (250 x 0.11 = 27.5, 250 x 0.1 = 25), and not to calculate them again every time.
Important Note: The questions on the SHL tests are taken from a pool of questions, so every candidate gets slightly different questions. As such, you might not find your EXACT questions in this guide. However, every type of SHL question is covered, so you should get a good idea of the correct answers for YOUR questions by following the techniques detailed in each question type.
We cannot help you cheat.
But we can help you ace your SHL Assessment.
Our preparation course is the fruit of years of helping candidates master SHL-type questions. It contains over 1,000 practice questions and is the leading internet resource for SHL guidance and preparation.
2. SHL Numerical Reasoning Test Question - Graphs and Tables #1

Final Answer:
To calculate yearly interest, we use the following formula:

This formula is a special case of the general formula to calculate change, this way:

Intuitively, we’re basically asking “how much more money do I have by the end of the year compared with what I had in the beginning, relative to the sum I had).
A very simple example to clarify this:
If I deposited $100 at the beginning of the year and ended with $110, then:

Year 1:

Tip: If you feel confident taking shortcuts, you may save time by dividing the entire formula by 10,000 for a more convenient calculation:

Year 2:

Remember! You should always use last year’s sum (in this case, $10,125), and not the initial sum (in this case, $10,000).
Year 3:

Putting the data on a graph, we gain:

3. SHL Numerical Reasoning Test Question - Graphs and Tables #2

Final Answer:
First, we notice that we are not given (nor are we requested to find) the actual budget of each department – only the percentages.
That means that we should calculate using the percentage data only.
To solve it in the best and fastest way, we will form 3 equations based on the data given for each department:
- Engineering - E + 2P = 76
- Product Delivery - P + F + 2M = 93
- Marketing - No Data
- Finance - 2F + 2P + 3M = 171
Where:
- E – Engineering budget
- P – Product Delivery budget
- F – Finance budget
- M – Marketing budget
Let’s rewrite the equations:
(1) E + 2P = 76 (%)
(2) P + F + 2M = 93 (%)
(3) 2F + 2P + 3M = 171 (%)
Now we have 4 equations in 4 variables to solve, where the last equation is, naturally:
(4) E + P + F + M = 100 (%)
(The entire company’s 100% budget is divided between the four departments).
Note: From now on, all numbers refer to percentages.
When approaching such a system of equations, the best thing to do is to take a moment and look at the equations, finding the combination to allow us to reduce the number of variables to 1.
Note that if we subtract Equation 3 from two times Equation 2, we are left only with variable M:
2 x (Equation 2) – (Equation 3) :
2 x (F + P + 2M) – (2F + 2P + 3M) =
2F + 2P + 4M – 2F – 2P – 3M = 2 x 93 – 171
So:
4M – 3M = 15
M = 15
Now, although we cannot find any other variable (E, F, or P) explicitly, we can explicitly express the combination F + P, and use equation 4 to find E:
From Equation 2:
P + F + 2M = 93
Plugging M = 15:
(P + F) + 30 = 93
So:
P + F = 63
Now, let’s plug both M = 15 and P + F = 63 into equation 4 to find E:
E + 63 + 15 = 100
E = 22
We now have M and E. the next step would be to look for an equation to plug those into and reveal a new variable (either P or F). for that, we can easily use Equation 1:
E + 2P = 76
22 + 2P = 76
2P = 54
P = 27
Tip: If we have 3 out of 4 variables, we can save time by NOT calculating the remaining variable (in this case, F). The interactivity of the pie chart will make sure that F is automatically derived from the last 3.
4. SHL Numerical Reasoning Test Question - Graphs and Tables #3
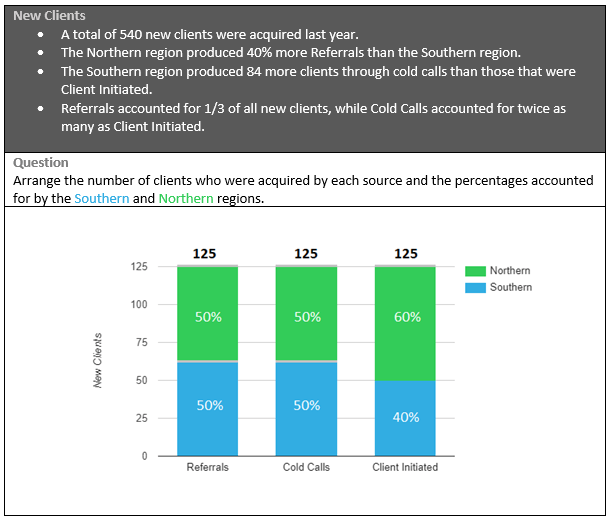
Final Answer:

Pretty similarly to question #3 in this guide – this one is a classic case of systems of equations used to find several variables.
In this case, we have 6 variables – let’s arrange them in a table for convenience:
| Variable | Region | Method |
| NR | Northern | Referrals |
| NC | Northern | Cold Calls |
| NI | Northern | Client-Initiated |
| SR | Southern | Referrals |
| SC | Southern | Cold Calls |
| SI | Southern | Client-Initiated |
Note: This table is for the sake of explanation only. During the real test, don’t spend time arranging it, and simply name the variables as is most convenient for you.
Out of the 4 data items, the first and last ones on the list are the best place to start, as they can immediately reveal the number of clients in each method.
Let’s dismantle these pieces of data to their components:
A total of 540 new clients were acquired this year
Referrals accounted for 1/3 of all new clients

Therefore, Cold Calls and Client-Initiated account for the remaining 2 thirds of new clients:
Cold Calls + Client-Initiated = 540 - 180 = 360
Using the last bit of information - Cold Calls accounted for twice as many as Client-Initiated:
2 (Client-Initiated) + Client-Initiated = 360
Client-Initiated = 120 Clients
Cold Calls = 240 Clients
So, we can now rearrange the graph as:

Tip: The pale grey lines above the graph means that you are able to change the value below the line. In this case, the total value of all bars can be changed, but the division of Client Initiated between Northern (60%) and Southern (40%) is pre-determined.
Now, let’s form some other equations using the other data items.
We should try and focus on data items containing the least variables. Data item 2 is the best for this purpose:
The Northern region produced 40% more Referrals than the Southern region.
Or in the form of an equation:
(I) NR = 1.4 x SR
We already know the total number of referrals:
(II) NR + SR = 180
Plugging (I) into (II):
2.4 x SR = 180
SR = 75
NR = 105
Converting to percentages (Don’t forget that!):

And again, we can rearrange the graphs as:

It is time to approach the last piece of information – data item 2:
The Southern region produced 84 more clients through cold calls than those that were Client Initiated.
Or in the shape of an equation:
SC = SI + 84
Since we already know the percentages in the Client-Initiated bar, we can easily deduce SI:
SI = 0.4 x 120 = 48
Plugging into the previous equation:
SC = 48 + 84 = 132
Again, converting into percentages:

And rearranging the graph to its final position:

5. SHL Numerical Reasoning Test Question - Graphs and Tables #4

Final Answer:

If you remember the tip regarding the pale grey lines from the previous question, you can immediately see that the number of people at School A is given as 200. That is also supported from data item 3.
Let’s start with data item 1 to determine the percentage of students and teachers at School A.
Since we need only the percentage and not the number of students and teachers at the school, we can consider the whole as 100 (percent), and not 200 (number of people).
Teachers : Students = 1 : 9
It is simple to deduce, then, that 90% of the school population are students, and 10% are teachers.
We shall rearrange the graph, then:

The only remaining data item is 2
School B has half as many students as School A and 10 more teachers.
We can immediately form the two equations:

Converting into percentages:

So, the final graph shall appear so:

6. SHL Numerical Reasoning Test Question - Graphs and Tables #5

Final Answer:

In this question, all the total numbers of phone owners are given, and we only need to determine the percentages of smartphone and non-smartphone users.
Tip: If you see one data item given per year, it is recommended to solve for one year at a time.
2010
Of the 200 million adults who owned cellphones in 2010, 70 million owned smartphones.
This data item gives a quick answer to the ownership division in 2010:

Let’s move on with the rest of the data and rearrange the graph in the end.
2014
By 2014, 230 million adults owned cellphones, and 56.5 million more adults owned smartphones than in 2010.
The first half of the sentence is already known (230 total cellphone owners). Let’s take a look at the second half, then:
By 2014… 56.5 million more adults owned smartphones than in 2010.
Quickly formulating an equation:

As ever, not forgetting to convert to percentages:
Tip: Remember that in percentage questions, you can save some precious seconds of calculating the complementary percentage (e.g., 45% in the example above). The interactivity of the question will make sure that both percentages sum up to 100%.
2018
In 2018, 250 million adults owned cellphones and non-smartphone users dropped by 72.5 million compared to 2010.
Again, we know the first half (250 million owners in 2018), so we regard only the second half of the data item:
In 2018…non-smartphone users dropped by 72.5 million compared to 2010.
This statement in the form of an equation yields:

Note that the 130 is derived from the calculation for 2010, in which we determined 70 million smartphone users out of 200 million total.
In percentage:

So, the final graph will be:

7. SHL Numerical Reasoning Test Question - Calculations #2

Final Answer:
- Order 1 - 5%
- Order 2 - 0%
- Order 3 - 5%
- Order 4 - 10%
This question is a simple question of matching conditions, let’s go very briefly over the solution:
Order 1
Since the contract length is longer than 6 months but shorter than 12, the discount can be either 0% or 5%. To figure out which, we should calculate the average monthly spending.

Therefore, the correct discount is 5%.
Note: The question requires that both terms regarding average monthly spending AND contract length of a specific type, must apply.
(E.g., average monthly spending of $30 or more AND a contract length of 12 months or longer for a discount rate of 10%).
Therefore, in this case (as mentioned earlier), as long as the average monthly spending is above $20, 5% discount will be given.
Order 2
The contract length is longer than 12 months, the discount can be any of the three discounts – 0%, 5%, or 10%. Again, we shall calculate the average monthly spending to determine.

Since we have average monthly spending of less than $20, the correct discount is 0%.
Orders 3 and 4
A fast way to solve the question is using a table, and we will demonstrate how to use it for orders 3 and 4:
| Order | Total Spending | Contract Length (Months) | Average Spending | Discount |
| Order 3 | $589 | 20 (More than 12) | $589 / 20 = $29.45 (Between 20 and 30) | 5% |
| Order 4 | $472 | 15 (More than 12) | $472 / 15 = $31.45 (More than 30) | 10% |
So, the final answer is:
- Order 1 - 5%
- Order 2 - 0%
- Order 3 - 5%
- Order 4 - 10%
8. SHL Numerical Reasoning Test Question - Ranking #1

Final Answer:
- Beatrice - 5
- Diana - 2
- Fei - 1
- Charlie - 6
- Edward - 4
- George - 3
To solve this question effectively and quickly, we will use one formula to find the desired metric, namely, the agent’s number of successful calls, and fill the data in a table, leaving the ranking to the end.
The formula is given by:

To find an agent’s number of successful calls, we need to divide the total time he or she spends on calls by the average call length:

Note: Pay attention to make all calculations in the same time unit (hours/minutes). For convenience, we will use minutes in this case (1 hour = 60 minutes).
We will show a detailed calculation for Beatrice:

So, Beatrice takes 72 calls a day, out of which 30% are successful – that is, 21.6 calls on average.
We will repeat the same process for all agents:
| Agent | Average Call Length | No. of Calls | Success Rate | Successful Calls | Rank |
| Beatrice | 5 min | 360/5 = 72 | 30% | 72 x 30% = 21.3 | 5 |
| Diana | 7 min | 51.4 | 75% | 38.55 | 2 |
| Fei | 6 min | 60 | 70% | 42 | 1 |
| Charlie | 4 min | 90 | 20% | 18 | 6 |
| Edward | 10 min | 36 | 80% | 28.8 | 4 |
| George | 6.5 min | 55.4 | 60% | 33.24 | 3 |
9. SHL Numerical Reasoning Test Question - Ranking #2

Final Answer:
- Edward - 6
- Diana - 4
- George - 1
- Beatrice - 2
- Fei - 5
- Phillip - 3
The best place to start is with the team member whose plants we know accurately and see what other team members can be expressed by it.
The only team member for whom we have a numerical value is Edward.
Edward = 160
Now, here comes a catch. Although it seems we can easily deduce Beatrice’s number of planted trees can be calculated using Edward’s data:
Beatrice planted a quarter of what Edward planted and a third of what George planted.
However, we still do not have enough data to calculate Beatrice’s plants, since we need George’s plants first (The word “and” here comes in the meaning of “plus”, and not in the meaning of “and also”).
At the end of the question, we will show the wrong calculation done for Beatrice.
Therefore, we will calculate for Diana first:
Diana planted a quarter of what Edward planted, plus 50 more.
Diana = (160/4) + 50 = 90
We can now calculate for George:
George planted half of the trees that Diana planted.
George = Diana/2 = 90/2 = 45
As we go back to Beatrice, we can understand that her data item means that she planted a quarter of what Edward did PLUS a third of what George did, namely:
Beatrice = (160/4) + (45/3) = 55
And we can now proceed to Fei:
Fei planted double what Beatrice planted.
Fei = Beatrice x 2 = 55 x 2 = 110
And lastly, Phillip:
Phillip planted half of what Fei planted, plus 20 more.
Phillip = (Fei/2) + 20 = (110/2) + 20 = 75
Now let’s sum everyone up, to see we did not make any calculation errors along the way:
160 + 90 + 45 + 55 + 110 + 75 = 535
Arranging the data in ranking order:
- Edward - 160 - 6
- Diana - 90 - 4
- George - 45 - 1
- Beatrice - 55 - 2
- Fei - 110 - 5
- Phillip - 75 - 3
Tip: Pay attention to the definition of the rankings! In some questions, such as this one, 1 will be defined as least, and 6 as most. In others (such as question 8), the opposite will be true.
Wrong solution for George and Diana:
Let’s assume Beatrice indeed planted a quarter of what Edward did (160), which is ALSO a third of what George did.
Beatrice = 160/4 = 40
And therefore:
George = Beatrice x 3 = 40 x 3 = 120
And Diana:
Diana planted a quarter of what Edward planted, plus 50 more.
Diana = 160/4 + 50 = 90
Now we will see if George’s data is satisfied:
George planted half of the trees that Diana planted.
George = 90/2 = 45
So, we have a contradiction, with 120 trees calculated from Beatrice’s data item, but 45 from George’s. Therefore, this solution cannot be correct.
10. SHL Numerical Reasoning Test Question - Calculations #3

Final Answer:
- Person A - Silver
- Person B - None
- Person C - Silver
- Person D - Gold
Ratings
Firstly, we know that in any case in which the average ratings are lower than 5, no award is given.

So, before calculating the sales, let’s first see which person deserves an award, to begin with – this will eliminate the need to calculate sales for persons with ratings lower than 5.
The average ratings are calculated simply as:
| Person | Average Ratings | Award |
| Person A | (4.5 + 5.5 + 5) / 3 = 5 | V |
| Person B | 4.33 | X |
| Person C | 5.16 | V |
| Person D | 5.33 | V |
Sales
Thanks to this pre-check of ratings, we now need to calculate sales for only 3 out of 4 persons.
To calculate how well the person has exceeded his or her sales goal, we use:

Forming a table again (remember that Person B receives no reward due to low ratings).
| Person | Sales Goal | Sales Achieved | Exceeded (%) | Award |
| Person A | $250 | $315 | (315 - 250) / 250 = 26% | Silver |
| Person C | $550 | $620 | 12.7% | Silver |
| Person D | $350 | $550 | 57% | Gold |
Remember – there is no need to waste time forming these tables in the actual test! The detailed tables are given here only for convenience and for explanatory purposes.
Feel Like You're Not Ready Yet?
Our SHL Numerical Interactive PrepPack contains comprehensive preparation materials, including:
3 Full-Length SHL Numerical Interactive Simulations - Mimicking the real SHL Numerical Exam, so you'll get to practice the real-time constraints, format, and difficulty level to determine your weak spots. Includes a tailored SHL Numerical Interactive guide.
30+ Additional Numerical-Focused Practice Tests - Allowing you to practice your weak spots and topics revealed in the simulations to improve your numerical skills and general readiness for the test. Our practice tests cover all questions and skills necessary to succeed in the SHL Numerical Test.
10+ SHL Study Guides & Video Tutorials - Giving you a professional grasp of the theory behind each test section and the best ways to solve questions.
For more free practice, check out our free SHL test!
SHL Talent Central Assessment Platform
The SHL Talent Central is an online platform that provides a wide range of pre-employment aptitude tests and psychometric tests for organizations to evaluate the aptitude, abilities, and potential of job candidates. This is the platform where you'll take your SHL Exam and your employers will see your results.
These tests help employers make more informed decisions on hiring, as well as provide a better understanding of their potential new employees. SHL Talent Central also provides a repository of resources such as tutorials and guides to help candidates prepare for the tests.
As a candidate taking the SHL numerical exam on the SHL Talent Central platform, here's what you need to know:
-
Access: You will receive an email from the employer or recruiter with a link to access the SHL Talent Central platform. Click on the link, and it will take you to the login page.
-
Login: You need to enter your login details, which may include your email address and a password provided by the recruiter or employer.
-
Test navigation: Once you log in, you will see the numerical reasoning test on your dashboard. You can start the test by clicking on the "Start" button.
-
Test duration: The numerical reasoning test is time-bound, and you will have a limited amount of time to complete it. The time count will be presented on the screen so make sure you're paying attention to it.
-
SHL Test results: Once you complete the test, your results will be available to the recruiter or employer who can access them on the platform.
Remember to prepare adequately for the test, manage your time wisely, and answer as many questions as possible within the allotted time. Good luck!
Create Your Custom Assessment Prep Kit
Job-seeking can be a long and frustrating process, often taking months and involving numerous pre-employment tests and interviews. To guide you through it, we offer a Premium Membership.
Choose 3 Preparation Packs at 50% discount for 1, 3, or 6 months.
Where Is This Practice Test Taken From?
On the SHL Direct website, you will find the numerical reasoning practice test at the top of the list. The link on your test invitation will also lead you there.
This is how the test list appears on the SHL Direct website:

Many prospective SHL test-takers find themselves on the SHL Direct website, taking SHL's practice test. The practice test provides no answers and/or explanations and leaves you only with a final score (at best). Therefore, this guide aims to:
- Let you know how well you did on the practice test.
- Let you know where you were wrong and how to improve.
- Provide you with tips and tools to ace the actual SHL Numerical Reasoning assessment.
Need More Practice?
Our SHL Numerical PrepPack includes 3 full-length interactive simulations that closely simulate the real exam's format, content, and time constraints. Along with these simulations, the package offers 30+ additional practice testscovering all types of questions you'll face in the exam. Additionally, the package includes 10+ study guides and video tutorials, providing a thorough understanding of the test's sections and the best methods to solve the questions.




